Contoh Penerapan Himpunan dalam Kehidupan Sehari-hari

Ngomong-ngomong soal himpunan, sebenarnya kamu bisa bayangkan kalau kamu datang ke kebun binatang di daerahmu. Di sana, kamu akan menemukan banyak jenis hewan. Kita akan membagi dua kelompok diantaranya hewan pemakan tumbuhan atau herbivora dan pemakan daging atau karnivora. 

Dari dua kelompok tersebut, berarti bisa dibuat seperti ini, contohnya: 

Himpunan hewan herbivora (pemakan tumbuhan saja) = {kelinci, kambing, rusa, kuda, orang utan, kera, beruang}

Himpunan hewan karnivora (pemakan daging saja) = {harimau, buaya, beruang, singa, kera, orang utan}

Kamu pasti akan menemukan hewan yang termasuk jenis pemakan tumbuhan dan daging diantaranya adalah beruang, orang utan dan kera. 

Nah, agar kamu bisa lebih memahaminya, yuk kita bahas satu persatu yang berhubungan dengan materi himpunan. 

Diagram Venn 

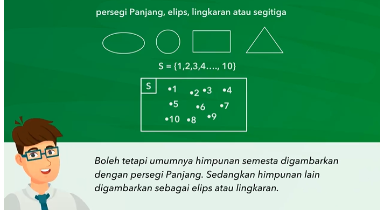
Sebelum membahas soal-soal himpunan, kita pahami terlebih dahulu tentang Diagram Venn. Diagram Venn adalah gambar yang menyatakan suatu himpunan terhadap himpunan semesta. Supaya lebih mudah dipahami, Diagram Venn bertugas memindahkan himpunan ke dalam bentuk gambar berupa lingkaran himpunan. Pada mulanya, Diagram Venn digunakan untuk menghubungkan relasi antar kelas. Jenis diagram ini pertama kali ditemukan oleh Bapak John Venn di Tahun 1880. 

Karakteristik Dari Diagram Venn 

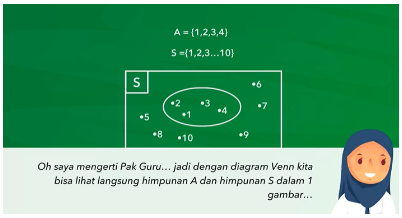
Diagram Venn memiliki beberapa ketentuan yang perlu kamu perhatikan, antara lain: 

S = Himpunan semesta. Pada umumnya digambarkan dengan persegi besar dengan simbol S di sudut kiri atas. 

A = Himpunan A yang merupakan himpunan lainnya. Himpunan ini digambarkan dengan lingkaran dalam persegi besar himpunan semesta. Dalam pengaplikasian soal, banyaknya lingkaran tidak hanya himpunan A saja.  Kamu akan menemukan soal lebih dari satu himpunan sehingga ada beberapa lingkaran dalam satu persegi besar. 

X = Himpunan yang tidak masuk dalam himpunan A. Pada Diagram Venn, jumlah anggota himpunan atau n(X) di tulis diluar lingkaran himpunan. 

Sedangkan simbol n merupakan jumlah anggota himpunan, contoh:  n(S), n(A) dan n(X). 

 

Jenis-Jenis bentuk Diagram Venn 

Diagram Venn memuat isi berupa data himpunan. Jenis-jenis Diagram Venn antara lain: 

 

Himpunan berpotongan 

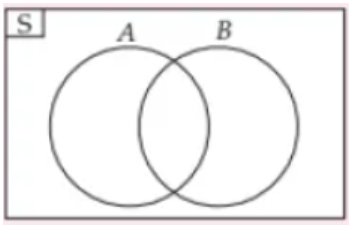
Himpunan berpotongan apabila ada anggota himpunan A yang juga termasuk anggota himpunan B. Jika dituliskan dalam simbol adalah A∩B. Himpunan ini bisa digambarkan dua lingkaran A dan B yang saling beririsan. 

Contoh A= {1,2,3,4,5]

             B= {4,5,6,7}

Jadi,anggota yang masuk kedua himpunan A dan B adalah 4 dan 5. 

Himpunan bagian

Contoh: S = {1, 2, 3, …, 10}

             A = {1,2,3, …., 8}

             B = {1,2,3} 

Himpunan B bisa dikatakan himpunan bagian  A.  Himpunan ini bisa digambarkan lingkaran B kecil yang masuk dalam lingkaran A besar.

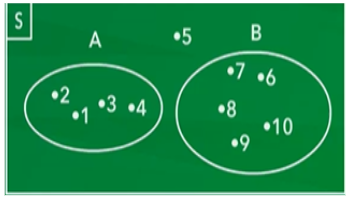
Himpunan Saling Lepas 

Himpunan ini terjadi karena anggota himpunan A tidak ada yang sama dengan anggota himpunan B. Himpunan ini bisa digambarkan dengan dua lingkaran A dan lingkaran B yang saling terpisah. Himpunan ini disimbolkan dengan A // B.
Contoh: 

S = {1, 2, 3, 4, .., 10}

            A = { 1, 2, 3, 4}
            B = {6, 7, 8, 9, 10}

Himpunan Sama 

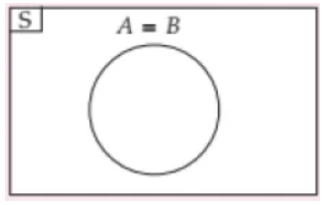
Himpunan ini terjadi karena anggota himpunan A merupakan anggota himpunan B, begitu juga sebaliknya. Himpunan ini bisa digambarkan dengan satu lingkaran saja dengan simbol A=B di atasnya. 

Contoh: A={Strawberry, Apel} 

             B={strawberry, Apel}

 

Himpunan Kosong

Himpunan kosong adalah himpunan yang tidak mempunyai anggota, dilambangkan dengan { } atau ∅ dengan n (A) = 0

contoh :

1. Himpunan A adalah himpunan siswa SD yang berusia 50 tahun.
2. Himpunan B adalah himpunan nama hari yang berawalan huruf “Z”.

A = B = { } karena tidak ada siswa SD yang berusia 50 tahun dan tidak ada nama hari yang dimulai dengan huruf Z.

Contoh Soal Cerita 1 Materi Himpunan

Tuliskanlah himpunan di bawah ini dengan mendaftarkan anggotanya: 

A = {Himpunan hewan berkaki empat}

B = {Himpunan daging buah berwarna merah}

C = {Himpunan kendaraan beroda dua}

D = [Himpunan alat tulis sekolah}

E = {Himpunan suku bangsa di Indonesia}

Dengan mendaftarkan anggotanya, maka himpunan-himpunan tersebut: 

A = {kucing, rusa, kambing, harimau, singa, anjing, …}. 

B = {strawberry, cherry, semangka, bit, jambu merah, tomat, …}. 

C = {sepeda gunung, sepeda motor, sepeda listrik, segway, otopet, motor balap, …}.

D = {bolpoin, pensil, penghapus karet, penggaris, jangka, penghapus tinta, …}. 

E = {Jawa, Batak, Bali, Asmat, Minang, Dayak, …}.

Contoh Soal Cerita 2 Materi Himpunan

Di dalam kelasmu sendiri terdapat 42 siswa. Suatu hari kamu ingin membuat grup Whatsapp yang sesuai dengan suku bangsa teman-temanmu untuk mengikuti lomba Budaya Indonesia. Setelah membuat grup, ditemukan 21 siswa bergabung di grup Jawa, 25 siswa bergabung di grup Batak, dan 7 siswa tidak berminat mengikuti lomba. 

 

Nah, pertanyaannya, bagaimana cara membuat diagram Venn dari soal cerita diatas. Lalu, kamu tentukan berapa jumlah kontak siswa yang gabung di grup Jawa dan Batak? Yuk, kita cari solusinya bareng-bareng. 

Solusinya dari Materi Himpunan yang Sudah Dipelajari

Pertama, kita tentukan dulu himpunan yang diketahui dari soal cerita diatas dengan simbol. Kamu bisa tulis seperti ini dulu: 

Diketahui: n {S} = jumlah himpunan semesta atau semua kelas= 42 siswa. 

      n {A} = jumlah siswa suku Jawa di kelas = 21 siswa. 

      n {B} = jumlah siswa suku Batak = 25 siswa.

      n {X} = Yang tidak mengikuti lomba = 7 siswa. 

      n sendiri merupakan simbol jumlah anggota dalam himpunan.

Dari sini, kamu cari dulu banyaknya siswa yang masuk di kedua grup itu. Bisa kamu hitung jumlah siswa yang mempunyai suku campuran Jawa dan Batak dengan rumus: 

     

n {A⋂B} = (n {A} + n {B}) – (n {S} –n{X}) 

n {A⋂B} = (21 + 25) – (42 –7)

n {A⋂B} = 11 

 

Akhirnya, kamu tahu ternyata jumlah siswa yang memiliki suku campuran Jawa dan Batak ada 11 orang. Jadi, 11 orang ini tergabung dalam dua grup, yaitu grup Jawa dan Batak. Setelah itu, kamu bisa lebih gampang menentukan jumlah siswa bersuku jawa saja dan batak saja. Dengan cara seperti ini: 

 

Siswa yang berasal dari suku Jawa saja = 21 – 11= 10 siswa. 

Siswa yang berasal dari Batak saja = 25 – 11= 14 siswa

 

Dari contoh di atas, beberapa pertanyaan mungkin ditanyakan dengan cara membolak-balikkan informasi yang belum diketahui, misalnya ditanyakan berapa siswa yang tidak berpartisipasi, berapa siswa yang berasal dari suku jawa saja, berapa siswa yang berasal dari suku batak saja atau berapa siswa yang terdapat pada suatu kelas tersebut. 

 

Kamu bisa mengerjakannya dengan mudah asalkan menggunakan rumus seperti diatas yaitu:

 

Jumlah yang suka kedua-duanya = (Jumlah himpunan 1 + Jumlah himpunan 2) – (Jumlah himpunan semesta – Jumlah anggota yang tidak berpartisipasi dalam himpunan.

n {A⋂B} = (n {A} + n {B}) – (n {S} –n{X}) 

 

Kamu bisa dengan mudah menjawab soal-soal tersebut dengan mengikuti Platform Alef 

dari Alef Education. Penasaran kan apa itu Platform Alef? 

Platform Alef merupakan platform pembelajaran online dari Alef Education yang bergerak di bidang pendidikan, isi konten platform ini membahas matematika khusus siswa MTs/ SMP kelas 7 secara gampang, asyik dan menyenangkan. Platform Alef sendiri banyak menyajikan video pembelajaran singkat untuk membantu kita lebih memahami matematika, juga dilengkapi permainan interaktif untuk menguji pengetahuan serta kuis-kuis latihan untuk membantu kita lulus ujian. Bagaimana sih cara mendapatkan akses Platform Alef? Caranya sangat mudah, cukup memberi tahu guru madrasah/sekolahmu tentang Platform Alef supaya mereka bisa mendapatkan kode akses di alef.co.id atau melalui Alef Success Coach di wilayahmu.